分析測試百科網 > 行業資訊 > 微信文章

一文讀懂PCA分析（原理、算法、可視化）內附Python作圖代碼

鹿明生物

2023.6.27

什么是PCA

PCA（Principal Component Analysis，主成分分析）是一種常用的降維技術，用于從高維數據中提取最重要的特征。它通過線性變換將原始數據映射到一個新的坐標系中，使得新的坐標系下的各個維度之間不相關，從而實現降維。

為什么要降維

設想一下,假如我有幾個學生的英語和數學成績，想要描述學生分數的整體情況，并將他們分入不同班級。那我也許只需要分成英語好數學差，數學差英語好以及都好都差這四個象限就行了。但是，如果我有許多學生許多門科目的成績呢？那么情況就非常復雜了，想要用一張圖描述這么多維度對三維生物來說就更不可能了。于是我就會想，要是能像只有兩門那樣簡單就好了，這時候就要用到降維了。通過主成分分析，可以將原始數據的維度減少到k維，同時保留了最重要的特征信息。降維后的數據在一定程度上簡化了計算和可視化，并且可以去除原始數據中的噪聲和冗余信息。主成分分析在數據預處理、特征提取和數據可視化等領域都有廣泛的應用。

PCA是怎么做的呢？

簡單來說：

1. 將坐標軸中心移到數據的中心，然后旋轉坐標軸，使得數據在C1軸上的方差最大，即全部n個數據個體在該方向上的投影最為分散。意味著更多的信息被保留下來。C1成為第一主成分。

2. 找一個C2第二主成分，使得C2與C1的協方差（相關系數）為0，以免與C1信息重疊，并且使數據在該方向的方差盡量最大。

以此類推，找到第三主成分，第四主成分……第p個主成分。p個隨機變量可以有p個主成分。這些主成分是原始數據的線性組合，可以用來表示原始數據中的信息。

大家聽懂了嗎？沒聽懂也沒有關系，我們直接來舉個低維的例子看看具體是怎么做的吧！

首先，我們建立一個三維直角坐標系

在里面撒上一些點，當然，每個點具有三個維度的（經過標準化的）觀測值。

計算每個點的每個維度的算術平均，我們得到所有點的重心（下圖中紅點）。

移動坐標系，使原點與重心重合。

接著，我們找到所有數據點的最優擬合直線，稱為PC1，將數據點投影上去，也就是說取過每個數據點（圖中為i）正交于PC1的直線與PC1的交點。

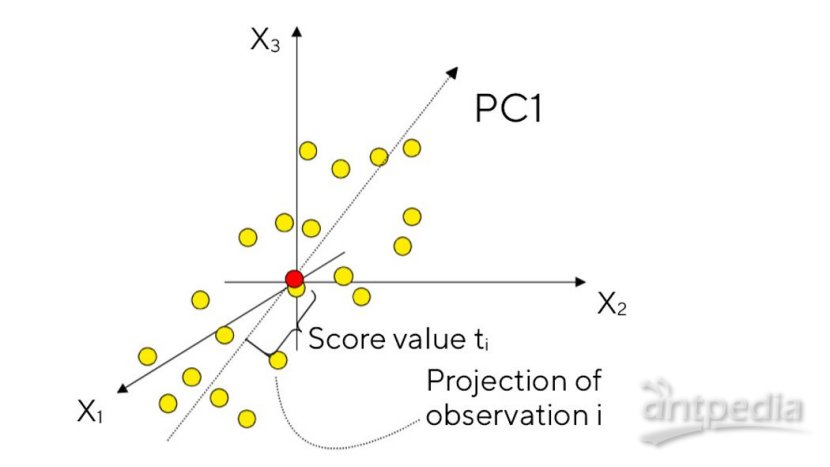
接下來再在與PC1正交的方向中找到一條最適回歸線經過原點，這樣就形成了一個平面（二維空間），然后通過數據點在PC1和PC2上的投影就能找到在平面上的投影。這樣一來，三維數據向二維的降維就完成啦！

作圖（Python代碼實現）

下面以sklearn.datasets內置的鳶尾花數據為例，展示用python代碼繪制有置信橢圓的散點圖。

import numpy as npfrom matplotlib.patches import Ellipseimport pandas as pdimport matplotlib.pyplot as pltimport randomfrom sklearn.decomposition import PCAimport matplotlib.pyplot as pltfrom sklearn.datasets import load_iris''''''用于計算樣本點的協方差矩陣''''''def plot_point_cov(points, nstd=3, ax=None, **kwargs): # 求所有點的均值作為置信圓的圓心 pos = points.mean(axis=0) # 計算協方差矩陣 cov = np.cov(points, rowvar=False) return plot_cov_ellipse(cov, pos, nstd, ax, **kwargs)''''''計算置信橢圓的參數''''''def plot_cov_ellipse(cov, pos, nstd=3, ax=None, **kwargs): # nstd=3代表99% 的置信區間 def eigsorted(cov): cov = np.array(cov) vals, vecs = np.linalg.eigh(cov) order = vals.argsort()[::-1] return vals[order], vecs[:, order] if ax is None: ax = plt.gca() # 計算輸入協方差矩陣的特征值和特征向量并返回排好序的結果 vals, vecs = eigsorted(cov) # 計算向量 vecs 的第一列的極角，并將結果轉換為角度制 theta = np.degrees(np.arctan2(*vecs[:, 0][::-1])) # 得到繪制的橢圓的寬度和高度 width, height = 2 * nstd * np.sqrt(vals) ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, **kwargs) ax.add_artist(ellip) return ellip''''''畫置信圓''''''def show_ellipse(X_pca, y, pca, flag=1): # 定義顏色 colors = [''tab:blue'', ''tab:orange'', ''seagreen''] regions = [''Ethiopia'', ''Somalia'', ''Kenya''] # 定義分辨率 plt.figure(dpi=300, figsize=(8, 6)) # 三分類則為3 for i in range(0, 3): pts = X_pca[y == int(i), :] new_x, new_y = X_pca[y==i, 0], X_pca[y==i, 1] plt.plot(new_x, new_y, ''.'', color=colors[i], label=regions[i], markersize=14) plot_point_cov(pts, nstd=3, alpha=0.25, color=colors[i]) # 添加坐標軸 plt.xlim(-3.5, 4.5) plt.ylim(-1.5, 1.7) plt.xticks(size=16, family=''Times New Roman'') plt.yticks(size=16, family=''Times New Roman'') font = {''family'': ''Times New Roman'', ''size'': 16} plt.xlabel(''PC1 ({} %)''.format(round(pca.explained_variance_ratio_[0] * 100, 2)), font) plt.ylabel(''PC2 ({} %)''.format(round(pca.explained_variance_ratio_[1] * 100, 2)), font) plt.legend(prop={"family": "Times New Roman", "size": 9}, loc=''upper right'') plt.show()labels = [''setosa'', ''versicolor'', ''virginica'']iris = load_iris() #讀入鳶尾花數據X = iris.datay = iris.target_names[iris.target]print("y length--------", len(y))y_category = pd.Categorical(y,ordered=True,categories=[''setosa'', ''versicolor'', ''virginica''])y = y_category.codesprint(y)print(y.shape)print(type(y[0]))n_components = 2 #為了繪圖方便，將PCA的主成分設為2pca = PCA(n_components=n_components) #PCA主成分分析X_pca = pca.fit_transform(X) #數據標準化show_ellipse(X_pca, y, pca)

產生的散點圖如上圖所示。比較重要的說明都寫成注釋標在代碼里了，值得注意的是，在函數plot_cov_ellipse中，nstd=3表示橢圓的長度和寬度分別擴展到 3 倍標準差的大小，覆蓋了大約 99.73% 的數據。這是因為在正態分布中，大約有 99.73% 的數據落在距離均值三個標準差的范圍內。因此，使用 nstd=3 繪制置信橢圓通常被認為是覆蓋 99% 的置信區間。如果需要95%的置信區間時可以將nstd設為2。但需要注意的是，這里所提到的百分比是基于正態分布的假設。

好了，今天關于PCA主成分分析作圖的分享就到這里了，趕緊把iris換成自己的數據集試試吧！祝大家在科研道路上一帆風順。

文末看點｜lumingbio

上海鹿明生物科技有限公司是歐易生物旗下從事蛋白質組及代謝組質譜檢測的專業質譜組學服務公司。公司建有國內第一個空間代謝組商業服務平臺，深耕質譜組學檢測分析，具體包括空間代謝組、雙平臺代謝組、靶向代謝組、TMT標記定量蛋白組、翻譯后修飾蛋白組、4D-DIA蛋白組、單細胞及超微量蛋白組、空間蛋白組等。創新質譜組學平臺廣泛應用于機制解析、分型診斷、標志物篩選、藥靶發掘等多個領域。公司并先后獲得高新技術企業、上海市專精特新企業并建有院士專家工作站，自有包括tims tof pro2在內的各類大型質譜近二十臺套，年服務項目超2000項。鹿明生物協助合作伙伴發表SCI論文近千篇，成功打造以硬數據、好服務為基礎，以空間代謝組為特色的質譜組學檢測服務公司品牌。